 From New Scientist #1225, 30th October 1980 [link] [link]
From New Scientist #1225, 30th October 1980 [link] [link]
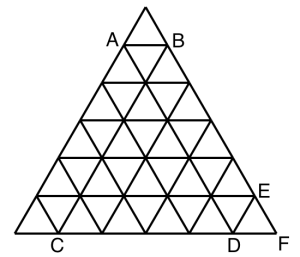
There are a lot of quadrilaterals in the figure; 492 in fact, I reckon. I do not count “crossed” quadrilaterals, like ABCD; only simple ones, like ABED, ABFD, and so on.
Now imagine the figure composed of 63 matches. My question is: what is the smallest number of matches you need to remove so as to spoil all 492 quadrilaterals? A quadrilateral is spoilt, of course, when one or more matches is missing from its boundary.
Interestingly, on the same page of New Scientist that this puzzle was originally published there is a review of the “sick, brutal and depraved” game – Missile Command.
[enigma82]


I found this a challenging problem to solve programatically, so I’ve added it to the list of Notable Enigmas.
My programmatic solution consists of two parts. The first identifies all the simple quadrilaterals in the array, and associates them with the set of matchsticks that make up the perimeter of each quad. It’s not particularly elegant, but I wanted to make sure it found the right set of quads (and it turns out this isn’t the time consuming part of the program).
The second part of the program involves finding a minimum set of matchsticks such that every quad is “spoit” by the removal of those matchsticks. This is a problem known as the Minimum Hitting Set problem, and is NP-hard, which means there is no easy shortcut to finding a solution.
I have used a simple recursive depth-first-search to find one of the minimum hitting sets. The only optimisation it uses is that it skips sets that are not smaller than the smallest it has already found. This is OK for a 5×5 array – it finds the solution in just under 4 minutes, but for the 6×6 array it takes a lot longer. I left it running overnight and it hadn’t even found a minimum solution.
However I wrote an augmented version of the algorithm, that represents the inclusion matrix of the quads and the matchsticks (matchsticks are columns and quads are rows) using bit vectors. This is coupled with the observations that any column that is a subset of another column can be removed and any row that is a superset of another row can be removed to reduce the problem at each step. This yields a solution to the 5×5 array in 30 seconds, but took nearly 22 hours to run to completion on the the 6×6 array (although it finds the solution much faster than that).
from itertools import product, combinations from enigma import irange, flatten, is_pairwise_distinct, Accumulator, printf # consider the grid to be made of points (x, y) for 0 < x + y < 7 # lines along x=n, y=n, x=y. # points reachable from p along each axis def points(p, n): (x0, y0) = p px = set((x, y0) for x in irange(0, n - y0) if x != x0) py = set((x0, y) for y in irange(0, n - x0) if y != y0) m = x0 + y0 pz = set((x, m - x) for x in irange(0, m) if x != x0) return (px, py, pz) # points on the line between p0 and p1 def line(p0, p1): if p0[0] == p1[0]: return set((p0[0], y) for y in irange(min(p0[1], p1[1]), max(p0[1], p1[1]))) if p0[1] == p1[1]: return set((x, p0[1]) for x in irange(min(p0[0], p1[0]), max(p0[0], p1[0]))) m = sum(p0) if m == sum(p1): return set((x, m - x) for x in irange(min(p0[0], p1[0]), max(p0[0], p1[0]))) # are the points collinear? def is_collinear(p0, p1, p2): return (p0[0] == p1[0] == p2[0] or p0[1] == p1[1] == p2[1] or sum(p0) == sum(p1) == sum(p2)) # do the points identify a non-crossing quad? def is_quad(p0, p1, p2, p3): return (is_pairwise_distinct(p0, p1, p2, p3) and # the lines (p0, p2) and (p1, p3) must not cross not(line(p0, p2).intersection(line(p1, p3)) or line(p0, p1).intersection(line(p2, p3))) and # check the none of the points are collinear not(is_collinear(p0, p1, p2) or is_collinear(p0, p1, p3) or is_collinear(p0, p2, p3) or is_collinear(p1, p2, p3))) # generate all quads on the n x n triangular array def quads(n): seen = set() # consider each point in the lattice for y in irange(0, n): for x in irange(0, n - y): p0 = (x, y) # extend the quad along two of the vertices for (i, j) in combinations(points(p0, n), 2): # consider points along these axes for (p1, p2) in product(i, j): # and the final point completes the quad for p3 in set(flatten(points(p1, n))).intersection(flatten(points(p2, n))): if not is_quad(p0, p1, p2, p3): continue q = tuple(sorted((p0, p1, p2, p3))) if q in seen: continue yield (p0, p1, p2, p3) seen.add(q) # return the set of edges on this line def edges(p0, p1): if p0[0] == p1[0]: return set((2 * p0[0], 2 * y + 1) for y in range(min(p0[1], p1[1]), max(p0[1], p1[1]))) if p0[1] == p1[1]: return set((2 * x + 1, 2 * p0[1]) for x in range(min(p0[0], p1[0]), max(p0[0], p1[0]))) m = sum(p0) if m == sum(p1): return set((2 * x + 1, 2 * (m - x) - 1) for x in range(min(p0[0], p1[0]), max(p0[0], p1[0]))) return set() # return the set of edges in this quad def quad_edges(q): (p0, p1, p2, p3) = q return edges(p0, p1).union(edges(p0, p2), edges(p1, p3), edges(p2, p3)) import sys N = 6 if len(sys.argv) < 2 else int(sys.argv[1]) # find all the quads on a 6x6 triangular array qs = list() for q in quads(N): # label the matchsticks (with an integer) m = set(e[1] + 2 * N * e[0] for e in quad_edges(q)) qs.append(m) printf("[quad {n}] {q} {m}", n=len(qs)) # find a minimum set that includes an element from each set in qs def solve(qs, s, r): # are we done? if len(qs) == 0: r.accumulate_data(len(s), s) printf("[size = {n}] {s}", n=len(s)) else: # choose an element from the first set for e in qs[0]: # if we might get a smaller solution if len(s) < r.value - 1: # solve for any remaining sets solve(list(q for q in qs if e not in q), s + [e], r) r = Accumulator(fn=min, value=len(qs)) solve(sorted(qs, key=len), list(), r) printf("min solution size = {r.value} {r.data}")Solution: The smallest number of matches that can be removed to spoil all quadrilaterals is 20.
Here is a diagram of one possible arrangement of the 20 matches (or, rather, the arrangement of the remaining 43 matches).
Note: The solution originally published with Enigma 85 gives an answer of 21 matches, but as can be seen above this can be improved upon. A corrected solution to this problem was published with Enigma 144 (although the diagram still shows 21 matches removed) and in the 1982 book Enigmas by Robert Eastaway (with a correct diagram).
The number of quadrilaterals in the n×n triangular arrangement of matchsticks is given by:
(see sequence A204185 in OEIS).
The number of matches that need to be removed to spoil all such quadrilaterals appears to be following sequence A000096 in OEIS, which has a general term of:
(which is a lot quicker to calculate than solving the Minimum Hitting Set problem).
The number of matchsticks in the arrangement with side n is 3n(n + 1)/2, three times the nth triangular number. No great surprise, as each right-way-up unit triangle has three sides, and the upside-down unit triangles contribute no additional matches.
The number of the latter is the (n – 1)th triangular number, n(n – 1)/2,
so the total number of unit triangles is n².
The number of triangles of all sizes (including the large bounding triangle) is
[n(n + 2)(2n + 1) – n mod 2]/8, or int[n(n + 2)(2n + 1)] if you prefer.
I modified my code that determines the quads to produce a data file for a simple GLPK model to find a Minimum Hitting Set, and glpsol solves the 6×6 case in 32.6s, so I might look at some of the Python/GLPK linkages to get a fully automated solution.
In the meantime here’s my GLPK model, and the data for the 2×2 case.
/* sets - the matches and the quads */ set MATCHES; set QUADS; /* parameters - the inclusion matrix */ param a {i in QUADS, j in MATCHES}; /* decision variables for the matches */ var x {j in MATCHES} binary >= 0; /* objective - minimum hitting set */ minimize size: sum{j in MATCHES} x[j]; /* constraint - the hitting set spoils each quad */ s.t. hit{i in QUADS}: sum{j in MATCHES} a[i,j] * x[j] >= 1; /* data for the 2x2 case */ data; set MATCHES := 1 3 100 101 102 103 201 300 301; set QUADS := 0 1 2 3 4 5; param a: 1 3 100 101 102 103 201 300 301 := 0 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 0 2 1 0 1 0 1 0 0 1 1 3 0 1 0 1 0 1 1 0 0 4 0 1 0 1 0 1 0 1 1 5 0 0 0 1 1 0 0 1 1; end;I installed PyMathProg, and once you’ve made a list of the quadrilaterals you can use this code to solve the Minimum Hitting Set problem over it. For the 6×6 case it runs in 52s, which is slower than using GLPK directly, but you do get the list of edges out of it in a more useful format.
import pymprog # return a minimum hitting set def mhs(qs): # elements of the universe (matches) ms = sorted(set().union(*qs)) # create the model p = pymprog.model('mhs') # decision variables - an x for each element x = p.var(ms, 'x', bool) # objective: minimise the size of the set p.min(sum(x[e] for e in ms)) # constraints: the set hits each quad p.st([sum(x[e] for e in q) >= 1 for q in qs]) # find a solution p.solve(int) # return the hitting set return list(e for e in ms if x[e].primal > 0) r = mhs(qs) printf("min size = {n} {r}", n=len(r))Running this GLPK model over the 7×7 case does indeed give a Minimum Hitting Set of size 27 (as predicted by A000096). glpsol ran for 3h57m, and found this solution.
As a precusor to using the fast Gurobi LP solver for this problem, I coded it for GLPK as follows. This requires my interface to GLPK which I make available here: http://cgi.gladman.plus.com/wp/glpk.py
from sys import argv from argparse import ArgumentParser from itertools import combinations from glpk import * # Enumerate the vertexes as: # # (0,0) 1 # (1,0) (1,1) 2 3 # (2,0) (2,1) (2,2) 4 5 6 # (3,0) (3,1) (3,2) (3,3) 7 8 9 10 # .... # the index for the vertex ar row r, position c in row def ix(r, c): return r * (r + 1) // 2 + c + 1 # list the vertex points in a formation with 'rows' rows def points(rows): pts = [] for r in range(rows + 1): for c in range(r + 1): pts.append((r, c)) return pts # four points are degenerate if three or more are on # the same line (and cannot form a quadrilateral) def degenerate(pts): for a, b, c in combinations(pts, 3): if (a[0] == b[0] == c[0] or a[1] == b[1] == c[1] or a[0] - a[1] == b[0] - b[1] == c[0] - c[1]): return True return False # check if two points are on a line that is aligned # with one of the three sides of the formation def aligned(p1, p2): return (p1[0] == p2[0] or p1[1] == p2[1] or p1[0] - p1[1] == p2[0] - p2[1]) # find all the quadrilaterals in the formation def quads(rows): # find all the vertex points p = points(rows) # now combine them four at a time # (note here that a < b < c < d) for t in combinations(p, 4): # check that they are not degenerate if not degenerate(t): a, b, c, d = t # ensure b is right of a if a[0] < b[0] and a[1] == b[1]: a, b = b, a # ensure d is right of c if c[0] < d[0] and c[1] == d[1]: c, d = d, c # now check that each pair of points lies on a # line aligned with a side of the formation if (aligned(a, b) and aligned(a, c) and aligned(b, d) and aligned(c, d)): yield (a, b, d, c) # find the set of individual segments on the line between # two vertex points with each segment identified by the # indexes of the two vertexes it is between def line_segs(a, b): if a[0] == b[0]: # they share a line parallel to the base return set(tuple(sorted((ix(a[0], i), ix(a[0], i + 1)))) for i in range(min(a[1], b[1]), max(a[1], b[1]))) elif a[1] == b[1]: # they share a line parallel to the left hand side return set(tuple(sorted((ix(i, a[1]), ix(i + 1, a[1])))) for i in range(min(a[0], b[0]), max(a[0], b[0]))) else: # they share a line parallel to the right hand side t = a[1] - a[0] return set(tuple(sorted((ix(i, t + i), ix(i + 1, t + i + 1)))) for i in range(min(a[0], b[0]), max(a[0], b[0]))) # list the segments on the perimeter of a quadrilateral def quad_segs(q): return (line_segs(q[0], q[1]) | line_segs(q[1], q[2]) | line_segs(q[2], q[3]) | line_segs(q[3], q[0])) # solve for a given number of rows def solve(rows): # list the segments on all quadrilaterals within # a formation with this number of rows constraints = [quad_segs(q) for q in quads(rows)] # compile a list of all segments segs = set() for s in constraints: segs |= s segs = tuple(sorted(segs)) # now map segment identifiers onto integers 1 .. size size = len(segs) inx = {s:(i + 1) for i, s in enumerate(segs)} xni = {(i + 1):str(s) for i, s in enumerate(segs)} # silence GLPK solver output glp_term_out(False) # create and name a GLPK minimisation problem lp = glp_create_prob() glp_set_prob_name(lp, 'New Scientist Enigma No 82'.encode()) glp_set_obj_dir(lp, GLP_MIN) # add a boolean variable for each individual segment glp_add_cols(lp, size) for i in range(1, size + 1): glp_set_col_name(lp, i, xni[i].encode()) glp_set_col_kind(lp, i, GLP_BV) glp_set_obj_coef(lp, i, 1) # now add each of the constraints glp_add_rows(lp, len(constraints)) for i, segs in enumerate(constraints): glp_set_row_name(lp, i + 1, str(i + 1).encode()) glp_set_row_bnds(lp, i + 1, GLP_LO, 1, 0) ix = [inx[s] for s in segs] glp_set_mat_row(lp, i + 1, ix, [1.0] * len(ix)) # solve the problem glp_simplex(lp) # for integer values glp_intopt(lp) # the minimum number of segments that have to be removed # to spoil all quadrilaterals n_segments = int(glp_mip_obj_val(lp)) # find the segments that have to be removed segs = [] for i in range(size): if glp_mip_col_val(lp, i + 1): segs += [glp_get_col_name(lp, i + 1).decode()] return n_segments, len(constraints), tuple(segs) n = int(argv[1]) if len(argv) > 1 else 6 print(solve(n))I have also coded this for the Gurobi solver and verified the values of 35 and 44 for 8 and 9 rows.
The LP tools I used to solve this puzzle 10 years ago have all succumbed to bit-rot and no longer work on my machine. But I tend to find myself using MiniZinc now when I want to make a declarative model to solve a puzzle, so here is the Minimum Hitting Set problem using MiniZinc (via my minizinc.py library).
I put the following code in the file utils_mzn.py:
from enigma import (union, sprintf as f, join) from minizinc import MiniZinc # find a minimum hitting set def hitting_set(ss, solver="minizinc", verbose=0): # find elements vs = sorted(union(ss)) # map elements to indices (1-indexed) m = dict((v, j) for (j, v) in enumerate(vs, start=1)) # construct the model model = [ # decision variables: x[j] = 1 if element j is in the hitting set f("array [1..{n}] of var 0..1: x;", n=len(vs)) ] + [ # each set must be hit f("constraint {sum} > 0;", sum=join((f("x[{j}]", j=m[v]) for v in s), sep=" + ")) for s in ss ] + [ # minimise the size of the hitting set "solve minimize(sum(x));" ] # execute the model (with additional arguments) for s in MiniZinc(model, solver=solver, verbose=verbose).solve(): xs = s['x'] # return the elements of the hitting set return set(vs[j] for (j, x) in enumerate(xs) if x == 1)And I wrote neater code to generate the quadrilaterals.
So here is a complete program to solve the puzzle using MiniZinc.
I found the
highssolver performed well (although it will only produce single answers, but in this case we only need one example of a minimum hitting set). For the size 6 grid it finds a solution in 3.8 seconds, and is able to run the size 7 grid in 23 seconds, the size 8 grid in 3 minutes, and the size 9 grid in 40 minutes.The
scipsolver performs better though. For the size 6 grid it finds a solution in 2.3 seconds, the size 7 grid takes 17.9 seconds, the size 8 grid takes 1 minute 39 seconds, the size 9 grid takes 11 minutes, and the size 10 grid takes 6 hours, 37 minutes.from enigma import (namedtuple, irange, subsets, ordered, cproduct, repeat, arg, printf) from utils_mzn import hitting_set # edge length of the triangular grid N = arg(6, 0, int) # a point has x and y values P = namedtuple("P", "x y") # points are non-negative (x, y) s.t. x + y <= N pts = set() for y in irange(0, N): pts.update(P(x, y) for x in irange(0, N - y)) # make a set of matchsticks from quad edges # each matchstick is of the form ((ax, ay), (bx, by)) def sticks(edges): ss = list() for (a, b) in edges: if a.x == b.x: ss.extend((P(a.x, y), P(a.x, y + 1)) for y in irange(a.y, b.y - 1)) elif a.y == b.y: ss.extend((P(x, a.y), P(x + 1, a.y)) for x in irange(a.x, b.x - 1)) elif a.x + a.y == b.x + b.y: ss.extend((P(a.x - k - 1, a.y + k + 1), P(a.x - k, a.y + k)) for k in irange(0, a.x - b.x - 1)) return ss # rotate a tuple of sticks rot = lambda ss: tuple(ordered(P(a.y, N - a.y - a.x), P(b.y, N - b.y - b.x)) for (a, b) in ss) # find quads quads = set() # choose a base level for the quadrilateral for y1 in irange(0, N - 2): # choose positions for the base points for (ax, bx) in subsets(irange(0, N - y1), size=2): # choose a top level for y2 in irange(y1 + 1, N - 1): k = y2 - y1 # choose position for the top points for (px, qx) in cproduct([[ax - k, ax], [bx - k, bx]]): if px < qx and P(px, y2) in pts and P(qx, y2) in pts: # find the matchsticks involved from the edges of the quadrilateral quad = sticks([ (P(ax, y1), P(bx, y1)), # base (P(px, y2), P(qx, y2)), # top (P(ax, y1), P(px, y2)), # left (P(bx, y1), P(qx, y2)), # right ]) # record all 3 rotations of the quadrilateral for qs in repeat(rot, quad, 2): quads.add(ordered(*qs)) printf("[N={N} -> {q} quads]", q=len(quads)) # find a minimum hitting set hs = hitting_set(quads, solver="minizinc --solver scip") printf("minimum hitting set size {n}", n=len(hs))Solution: The smallest number of matches that can be removed to spoil all quadrilaterals is 20.